Abbildung 1.0: Erde und Mond.

Die Menschen sind Erdbewohner, und - mindestens bislang - von kurzen Hüpfern abgesehen, an die Erde als Raumschiff und Lebensinsel gebunden. Der Mond ist der einzige Himmelskörper, der bislang von Menschen betreten wurde (es waren allesamt Männer und Amerikaner). Man kann also sagen, dass die Erde für uns eine zentrale Bedeutung hat, so dass es sich anbietet, unsere kleine Reise durch die grosse Welt hier zu beginnen. Der Mond, zusammen mit der Sonne der scheinbare grösste Himmelskörper, bietet sich aufgrund seiner mannigfachen Einflüsse und seiner Nähe als zweiter “Startpunkt” an.

In diesem Kapitel:

• Wer um wen?
• Wie lange braucht der Mond um die Erde?
• Wie weit ist der Mond entfernt?
• Wie gross?
• Wie “schwer” ist die Erde und der Mond?
• Hat der Mond eine Atmosphäre?
• Gezeiten und das Leben auf der Erde
• Übung: Wie hoch sind die Mondberge?

Wer um wen?

Dreht sich der Mond um die Erde oder die Erde um den Mond oder beide umeinander? Woran kann ich das erkennen?

Beginnen wir mit einigen Beobachtungen. Der Mond bietet ein besonderes Schauspiel: er ist manchmal kreisförmig (Vollmond), manchmal halbkreisförmig (Halbmond, zu- und abnehmend), wobei ihm von mittleren Breiten aus betrachtet mal die rechte, mal die linke Seite “fehlt” und dann ist er noch für einige Nächte unsichtbar (Neumond) (siehe Abbildung 1.1). Aufmerksame Beobachter bemerken, dass der Mond jede Nacht zu einer etwas späteren Zeit aufgeht, oder, wenn man immer zur gleichen Uhrzeit beobachtet, immer ein wenig weiter ostwärts steht als in der Nacht zuvor. Weiter haben viele Leute bereits einmal eine Mondfinsternis beobachtet, wenn der volle Mond sichelförmig überdeckt wird und schliesslich - bei einer totalen Mondfinsternis - schwach rötlich leuchtet, um anschliessend das gleiche Schauspiel seitenverkehrt zu bieten, bis wieder die ganze, hellgrau leuchtende, kreisförmige Fläche zu sehen ist. Seltener sind Sonnenfinsternisse, bei welchen sich die Sonne verdunkelt und - sehr selten - ganz verschwindet. Diese Ereignisse finden nur bei Neumond statt, wenn der Mond während der Nacht nicht sichtbar ist.

  

Abbildung 1.1: Schematische Darstellung der Mondphasen. Die Sonne steht rechts. Bei Neumond ist nur die unbeschienene Seite des Mondes der Erde zugewandet, welche am Tageshimmel kaum auszumachen ist. Sie wird ein wenig von der Rückstrahlung der Erde aufgehellt, so dass sie in Teleskopen beobachtbar ist. Beim Lauf des Mondes um die Erde wird erst eine dünne Sichel sichtbar, die mit jedem Tag zunimmt. Beim zunehmenden Halbmond steht der Mond von der Erde aus gesehen genau senkrecht zur Sonne. Vollmond ist, wenn der Mond von der Erde aus gesehen auf der entgegengesetzten Seite der Sonne steht. Da die Mondbahn nicht genau in der gleichen Ebene wie die Bahn der Erde um die Sonne liegt, gibt es nicht bei jedem Vollmond eine Mondfinsternis. Vom Vollmond an läuft der Mond wieder Richtung Sonne und verkleinert seinen sichtbaren Teil mit jedem Tag.

Daraus können wir bereits einige Schlüsse ziehen: offenbar leuchtet der Mond also nicht selbst (sonst müsste es einen komplizierten Helligkeitsregler geben, um die Mondphasen zu erklären), sondern reflektiert nur Licht, dass von der Sonne kommt (die Sonne als hellster Himmelskörper bietet sich als Leuchte geradezu an, oder nicht?). Somit kann man zwei Arten von Modellen bauen, in welchen die drei Körper, Erde, Sonne und Mond, umeinanderkreisen: entweder ist die Erde im Mittelpunkt, und wird vom Mond und noch weiter aussen von der Sonne umkreist (das ist das antike, oft Ptolemaisch genannte, Weltbild, welches bis zum 16. Jahrhundert als richtig angesehen wurde.), oder die Sonne steht im Zentrum und wird von der Erde umkreist, um die wiederum der Mond kreist. Im letzteren Fall könnte es auch andersrum sein: der Mond kreist um die Sonne und wird von der Erde umlaufen. Warum sollte nicht das der Fall sein? Den Hinweis liefern die Häufigkeiten von (totalen) Mond- und Sonnenfinsternissen sowie die Tatsache, dass Sonnenfinsternisse vom Beobachtungsort abhängen. Das bedeutet nämlich, dass der Schatten, den der Mond auf die Erde wirft, kleiner ist als der Schatten, den die Erde auf den Mond wirft. Der Mond verschwindet ganz im Erdschatten, der Mond verdeckt die Sonne aber nur für einen kleinen Punkt auf der Erdoberfläche von bestenfalls einigen hundert Kilometer Durchmesser. In der Abbildung 1.2 ist der Zusammenhang dargestellt.

  

Abbildung 1.2: Anhand von Sonnen- und Mondfinsternissen kann man ableiten, wer der grössere Partner ist.

zum Seitenkopf, zum Inhaltsverzeichnis dieser Seite

Wie lange braucht der Mond um die Erde?

Die Rotationsperiode des Mondes um die Erde haben bereits die Babylonier auf ein paar Stellen hinter dem Komma genau bestimmt. Wie kann man das selber machen?

Eine Möglichkeit ist, die Zeit von Vollmond zum nächsten Vollmond (oder, einfacher, von Neumond zu Neumond) zu messen. Eine andere, die Position des Mondes an einem Tag zu einer bestimmten Zeit zu bestimmen, und 24 Stunden später die Position des Mondes relativ zu den Sternen nochmals zu bestimmen (der Mond ist etwa 12 Grad weiter östlich anzutreffen). Mit dem gemessenen Winkel kann man die Zeit bestimmen: einmal um die Erde herum sind eine Drehung um 360 Grad; 360 / gibt die Zeit in Tagen. Diese Art von Messung ergibt den sogenannten Synodischen Monat (das Wort Monat stammt übrigens von “Mond” ab). Der heute gültige Wert ist 29.530589 Tage.

Es gibt noch andere Arten von (Mond)Monaten, die hier nur der Vollständigkeit halber erwähnt werden sollen: den siderischen Monat mit einer Länge von 27.3 Tagen (der Mond passiert einen Stern nahe der Ekliptik), den tropischen Monat (der Mond passiert zwei Mal aufeinander folgend den Frühlingspunkt) und den drakonitischen Monat (der Mond passiert zwei Mal aufeinander folgend den aufsteigenden Knoten. Als Knoten bezeichnet man die beiden Schnittpunkte der Mondbahn mit der Ebene der Erdumlaufbahn um die Sonne).

zum Seitenkopf, zum Inhaltsverzeichnis dieser Seite

Wie weit ist der Mond entfernt?

Die Entfernung zum Mond kann man aus der so genannten täglichen Parallaxe oder einer etwas modifizierten Form davon bestimmen. Das ist in Abbildung 1.3 dargestellt.

  

Abbildung 1.3: Bestimmung der Entfernung zum Mond mittels der “täglichen Parallaxe”. Zwei Beobachter auf der Erde in einem möglichst grossen Abstand zueinander messen den Winkel , den ein bestimmter Punkt am Mond, z.B. ein Berggipfel, von ihrem Beobachtungspunkt aus hat. In der Regel wird man den Winkel in einem astronomischen Koordinatensystem angeben, das letztlich an den Hintergrundsternen “aufgegängt” ist. Wenn man den geradlinigen Abstand der beiden Beobachter aus den Koordinaten der Beobachter bestimmt hat (nicht die Weglänge an der Erdoberfläche entlang!), kann man mit dem gemessenen Winkel den Abstand zum Mond berechnen.

Heute kann man die Entfernung des Mondes entweder mit Radar- oder Laserlichtlaufzeit extrem präzise bestimmen. Dazu sendet man ein Radarsignal oder einen Laserstrahl auf den Mond und wartet, wie lange es dauert, bis die Reflektion zurückkommt. Es sind etwas mehr als 2 Sekunden. Der Wert der mittleren Entfernung Erde-Mond ist 384401 km.

zum Seitenkopf, zum Inhaltsverzeichnis dieser Seite

Wie gross?

Es ist ein interessanter Zufall, dass Mond und Sonne von der Erde aus praktisch gleich gross aussehen, etwa 0.5 Grad (aus diesem Grund gibt es Sonnenfinsternisse). Tatsächlich ist die Sonne viel grösser als der Mond, nur ihre scheinbaren Grössen sind gleich. Der Effekt der scheinbaren Grössen oder Winkelgrössen ist in der Grafik 1.4 gezeigt. Wie gross sind nun aber die Erde und der Mond?

  

Abbildung 1.4: Die scheinbare Grösse hängt vom Abstand des beobachteten Objektes ab. Der Winkel, unter dem das Objekt erscheint, bleibt dabei aber immer gleich. Eine Münze in 10 cm Entfernung vom Auge ist so gross wie ein Haus in 100 m Entfernung, der Mond in etwa 400000 km, die Sonne in 1.5 Millionen Kilometern und eine grosse Galaxie in 3 Megaparsec (knapp 10 Millionen Lichtjahre).

Für die Erde ist eine gute Schätzung bereits von Erathostenes (geboren 273 vor Christus), einem Philosophen aus Alexandria, gemacht worden. Er mass dazu die Länge des Schattens eines senkrecht in die Erde gerammten Stabes in Alexandria (zusammen mit der Länge des Stabes ergibt sich der Winkel, unter dem die Sonne zu dieser Zeit in Alexandria vom Zenith weg stand) an genau dem Tag, an welchem in Assuan (seinerzeit Syene) die Sonne genau im Zenit, also exakt senkrecht über dem Ort, stand. Mit diesem Winkel und der Entfernung von Assuan nach Alexandria konnte er den Erdumfang zu ziemlich genau 40000 km bestimmen (man beachte, dass es man besser nicht entlang eines Breitenkreises misst). Der genaue Wert des Erathostenes ist allerdings etwas interpretationsfähig, da die Längeneinheit der Stadien, die er benutzte, von der Genauigkeit der Schrittlänge eines Mannes abhing, der die Länge eines Stadions abschritt. Der heutige Wert für den mittleren Erdumfang ist 40030 km, der Äquatorumfang ist 40075 km.

Vom Mond kann man direkt nur die scheinbare Winkelgrösse messen. Um daraus seinen tatsächlichen Durchmesser zu berechnen, müssen wir die Entfernung kennen, die wir bereits zu etwa 384000 km bestimmt haben. Mit dem mittleren scheinbaren Durchmesser von 31 Bogenminuten erhält man so den Monddurchmesser. Der heute gültige Wert ist 3476 km.

zum Seitenkopf, zum Inhaltsverzeichnis dieser Seite

Wie “schwer” ist die Erde und der Mond?

Wenn wir die Umlaufzeit und den Abstand Erde-Mond kennen, dann können wir dank des dritten Keplerschen Gesetzes (aus dem Jahr 1618, als auch der dreissigjährige Krieg begonnen wurde mit dem Ziel, aus Mitteleuropa eine Wüste zu machen im Namen Gottes) die Masse von Erde und Mond berechnen (für mathematisch nicht Abschreckbare folgt die Formel):

 

(1.1)

Eine andere Möglichkeit zur Massenbestimmung des Gesamtssytems Erde und Mond ist, für Kreisbahnen (was im Fall Erde-Mond nicht wirklich stimmt, aber eine gute “Näherung” ist) das Keplerproblem aus “Energiesicht” zu betrachten: die Anziehungskraft der beiden Massen muss gleich gross sein wie die Zentrifugalkraft (wäre die Anziehungskraft grösser, würden die beiden aufeinanderknallen; wäre sie kleiner, würden sie voneinander wegfliegen). Als Formel geschrieben:

 

(1.2)

Natürlich werden wir kein sehr genaues Ergebnis erhalten. Aber in der Astronomie wie auch sonst im Leben ist es oft sehr nützlich, “schnell” mal eine Abschätzung zu machen. Fangen wir also einmal an: die mittlere Entfernung Erde-Mond haben wir oben zu 384401 km angegeben. Für unsere Zwecke reicht eine runde Zahl: a = 400000 km = m. Die Gravitationskonstante m³kg^-1s^-2 und . Letzteres brauchen wir, um die Geschwindigkeit des Mondes v auszurechnen: die Länge der Mondbahn als Kreisbahn ist m. Dazu braucht der Mond 27.3 Tage oder s s. Damit ist seine Geschwindigkeit m/s. Wenn wir das einsetzen in die Gleichung 1.2, erhalten wir für die Masse:

M	=		(1.3)
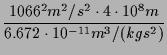			(1.4)
	=		(1.5)

zum Seitenkopf, zum Inhaltsverzeichnis dieser Seite

Hat der Mond eine Atmosphäre?

Der Mond hat keine Atmosphäre wie die Erde. Das kann man bereits an zwei Effekten erkennen: erstens gibt es bei Vollmond keine zunehmende Kontraständerung (Verschwimmen) oder Eintrübung von der Mitte zum Rand. Hätte der Mond eine dichte Lufthülle, so müsste man einen solchen Effekt beobachten, weil die Sichtlinie am Rand einen weiteren Weg durch die Atmosphäre zurücklegen muss als in der Mitte (siehe Abbildung 1.5). Der beschriebene Effekt müsste auftreten, weil Gas das Licht streut. Aus dem Grund kann man auf der Erdoberfläche auch nicht beliebig weit sehen, sondern meistens weniger als 150 km weit. Auf hohen Bergen weiter, weil die Luft dort dünner ist. Ausserdem ist die Sichtweite noch von der Art des Luftgemisches abhängig: bei Nebel oder Smog sieht man weniger weit.

  

Abbildung 1.5: Hätte der Mond eine Atmosphäre, würde man eine “Randeintrübung” beobachten, weil das Licht vom Rand einen weiteren Weg durch die Lufthülle zurücklegen müsste und dabei mehr Licht verloren geht als in der Mitte.

Der zweite Effekt ist bei Sternbedeckungen durch den Mond zu beobachten: hätte der Mond eine dichte Atmosphäre, dann müsste das Sternlicht umso schwächer werden, je näher der Stern an die Mondoberfläche kommt, weil das Sternlicht in der Atmosphäre gestreut wird. Das tritt aber nicht auf. Stattdessen verschwinden die Sterne “plötzlich”.

Weil der Mond keine Atmosphäre hat, sind die Temperaturunterschiede zwischen der beleuchteten Seite und der abgewandten Seite sehr viel grösser als auf der Erde. Die Erdatmosphäre enthält sogenannte Treibhausgase, vor allem Wasser und Kohlendioxid, die Wärme speichern können. Zudem ist ein Mondtag mit 27.3 Tagen deutlich länger als ein Erdtag, so dass für das Aufheizen und Abkühlen mehr Zeit bleibt. Insgesamt schwankt die Temperatur auf der Mondoberfläche um etwa 250 Grad, von bis .

zum Seitenkopf, zum Inhaltsverzeichnis dieser Seite

Gezeiten und das Leben auf der Erde

Die Anziehungskraft von Erde und Mond ist wechselseitig: das ist die Aussage von Isaac Newtons drittem Gesetz “Actio gegengleich Reactio” (Isaac Newton lebte von 1642 bis 1727 in England; er gilt als einer der grössten Wissenschaftler aller Zeiten). Die grössere und schwerere Erde zieht also nicht nur den Mond an, sondern der Mond auch die Erde. Durch die Anziehungskraft des Monds auf die Erde kommt es zu den Gezeiten: am besten deutlich werden sie in ihrer Wirkung auf die Wassermassen der irdischen Ozeane. Auf der dem Mond zugewandten Seite beobachten wir einen Flutberg, auf der Mond abgewandten Seite ebenfalls einen “Wasserberg”, der durch die Zentrifugalkraft bewirkt wird. Für Küstenbewohner von offenen Meeren äussert sich die Gezeitenwechselwirkung in Form von Ebbe und Flut. Siehe Abbildung 1.6.

  

Abbildung 1.6: Schematische Darstellung der Gezeitenwechselwirkung zwischen Erde und Mond. Auf der mondzugewandten Seite wird der Flutberg durch die Anziegungskraft des Mondes erzeugt, auf der mondabgewandten Seite durch die Fliehkraft.

Die Gezeitenwechselwirkung verursacht aber nicht nur Ebbe und Flut, sondern verformt auch die Atmosphäre und sogar den “festen” Boden unter unseren Füssen. Tatsächlich schwimmt die Erdkruste, der “feste” Boden, auf dem zähflüssigen Erdmantel. Die Erde ist also kein wirklich starrer Körper. Und die Ursache davon ist gerade die Einwirkung des Mondes auf die Erde, denn durch die Verformung des Erdballes, die immerhin etwa 35 cm (die Sonne trägt auch noch etwa 15 cm bei, so dass bei Neumond etwa 50 cm resultieren) auf den Kontinenten beträgt, entsteht aufgrund der Reibung Wärme, die verhindert, dass das Erdinnere so schnell abkühlen kann wie es beispielsweise bei der fast gleichgrossen Venus der Fall war.

Diese innere Wärme hat einige Konsequenzen. Erstens wird dadurch die Plattentektonik ein Thema im Geografieunterricht, denn die Bewegung der Kontinentalplatten könnte nicht auftreten, wenn die Erdkruste sehr dick wäre. Die Kontinentaldrift, die zum Beispiel zwischen Afrika und Südamerika etwa 2 m pro 100 Jahre beträgt, ist auch für die Entstehung der Faltengebirge wie den Alpen, des Himalaya, Anden oder den Rocky Mountains an den Nahtstellen zwischen den Kontinentalplatten verantwortlich. Diese Zonen sind auch die Entstehungszonen von Erdbeben. Zweitens, nicht ganz unabhängig vom ersten Punkt, gibt es darum Vulkanismus auf der Erde. Vulkane treten vor allem an den Nahtstellen der kontinentalen Schelfe auf und manchmal auch an “Löchern” in der Erdkruste. Der dritte Punkt ist der wichtigste aus Sicht des “Landlebens” auf der Erde. Da das Erdinnere zum grössten Teil noch flüssig und heiss ist, kann durch einen Dynamoeffekt ein Magnetfeld erzeugt werden. Dieses Erdmagnetfeld schützt uns vor hochenergetischer Teilchenstrahlung, vor allem vor dem Sonnenwind. Es lenkt diese Teilchen entlang seiner Feldlinien ab, und weil diese in etwa mit den geografischen Polen übereinstimmen, kann man in den Polargebieten die Wechselwirkung dieser Teilchen mit den Luftmolekülen der Erdatmosphäre als Polarlichter bewundern. Da die anderen Gesteinsplaneten, vor allem Venus und Mars, nur unbedeutende Magnetfelder besitzen, wären Kolonialisten dort auf Abschirmungsanlagen angewiesen oder auf ein Leben unter der Oberfläche.

zum Seitenkopf, zum Inhaltsverzeichnis dieser Seite

Übung: Wie hoch sind die Mondberge?

Die Höhe der Mondberge kann man aus der Länge ihrer Schatten bestimmen. Ausser bei Vollmond werfen aufgrund des streifenden Lichteinfalls alle Unebenheiten der Mondoberfäche, Berge und Krater, Schatten. Am längsten sind die Schatten bei Halbmond entlang des “dunklen” Randes des Mondes zu messen.

  

Abbildung 1.7: Darstellung der Geometrie der Mondberghöhenbestimmung.

In der Abbildung 1.7 erkennt man den Zusammenhang der Grössen R (Radius des Mondes), l (Abstand vom Terminator, der Trennlinie zwischen Hell und Dunkel), s (Schattenlänge) und h (Höhe des Mondberges/Kraters aufgrund der Ähnlichkeit der Dreiecke:

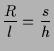(1.6)

(1.7)

Kann man eine Aussage treffen, ob die Mondkrater Vulkankrater oder Einschlagskrater sind? An was könnte man das erkennen?